参数估计的类型有

A.
点估计和无偏估计

B.
点估计和区间估计

C.
点估计和有效估计

D.
无偏估计和区间估计
A,B满足P(A)+P(B)>1,则A,B一定( )

A.
不相容

B.
相容

C.
独立

D.
不独立
当X服从参数为n,p的二项分布时,P(X=k)=( )

A.
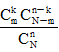

B.
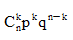

C.
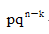

D.
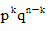
随机地掷一骰子两次,则两次出现的点数之和等于8的概率为( )

A.
2/36

B.
4/36

C.
3/36

D.
5/36
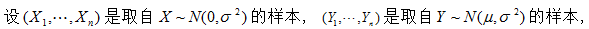
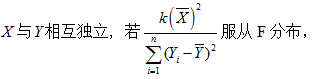 自由度是
自由度是

A.
1,n-1

B.
1,n

C.
n-1,n-1

D.
1,1
A,B两事件,若 P(AUB)=0.8,P(A)=0.2,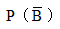 =0.4,则下列( )成立.
=0.4,则下列( )成立.

A.
P(AB)=0.4

B.
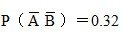

C.
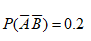

D.
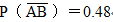
已知 EX=-1, DX=3,则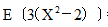 =( )
=( )

A.
30

B.
9

C.
36

D.
6
甲乙是两个无偏估计量,如果甲估计量的方差小于乙估计量的方差,则称

A.
甲乙一样有效

B.
甲是充分估计量

C.
乙比甲有效

D.
甲比乙有效
从数1,2,3,4中任取一个数,记为X,再从1,2,...,X中任取一个数,记为Y,则P{Y=1}=( ).

A.
1/16

B.
1/4

C.
25/48

D.
13/48
设随机变量X的方差存在,则( )

A.
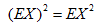

B.
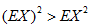

C.
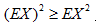

D.
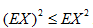
一电话交换台每分钟接到的呼唤次数X服从的泊松分布,那么每分钟接到的呼唤次数大于20的概率是( )

A.
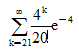

B.
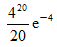

C.
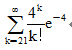

D.
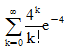
已知 P(A)=0.8, P(A-B)=0.2, 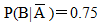 ,则P(B)=( )
,则P(B)=( )

A.
0.4

B.
0.5

C.
0.75

D.
0.6
若二事件A和B同时出现的概率P(AB)=0,则( )

A.
P(A)=0或P(B)=0

B.
AB未必是不可能事件

C.
A和B不相容(相斥)

D.
A,B是不可能事件
在假设检验中,第一类错误是指

A.
当备择假设不正确时未拒绝备择假设

B.
当原假设错误时拒绝原假设

C.
当原假设正确时拒绝原假设

D.
当备择假设正确时未拒绝备择假设
设F(x)是随机变量X的分布函数,则对( )随机变量X,有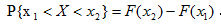

A.
个别离散型

B.
连续型

C.
离散型

D.
任意
X为连续型随机变量,p(x)为其概率密度,则( )

A.
p(x)=F(x)

B.
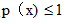

C.
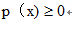

D.
P(X=x)=p(x)
设p(x.y)为(X,Y)的联合密度函数,则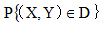 等于( )。其中D由 y=2x ,x=1, y=0所围
等于( )。其中D由 y=2x ,x=1, y=0所围

A.
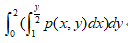

B.
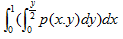

C.
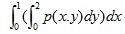

D.
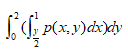
下列函数可作为概率密度的是( )

A.
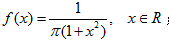

B.
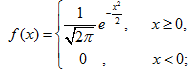

C.
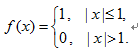

D.
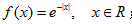
设连续型随机变量X的分布函数为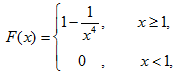 则X的数学期望为( )
则X的数学期望为( )

A.
0

B.
8/3

C.
2

D.
4/3
设二维离散型随机变量(X,Y)的分布律为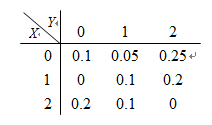 ,则( )
,则( )

A.
X,Y独立且相关

B.
X,Y不独立

C.
X,Y独立

D.
X,Y不相关
- 第2部分
- 总题数: 5
下式中正确的是
 A.
A.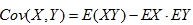
 B.
B.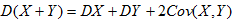
 C.
C.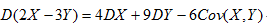
 D.
D.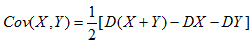
设A,B为任意两个事件,下列说法正确的是
 A.
A.若,则A与B相互独立
 B.
B.若P(A)=0,则A与B相互独立
 C.
C.若,则A与B相互独立
 D.
D.若P(A)=1,则A与B相互独立
下列哪些可以作为某个随机变量的分布律
 A.
A.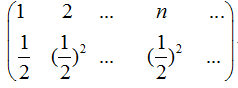
 B.
B.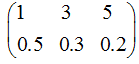
 C.
C.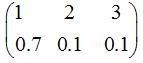
 D.
D.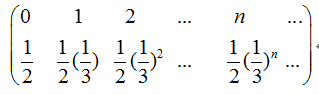
下列关于二项分布的结论正确的是
 A.
A.
 B.
B.
 C.
C.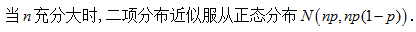
 D.
D.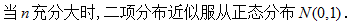
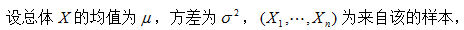 则在下列估计量中哪些为
则在下列估计量中哪些为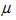 的无偏估计
的无偏估计
 A.
A.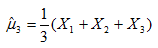
 B.
B.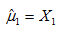
 C.
C.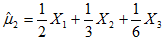
 D.
D.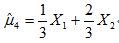
- 第3部分
- 总题数: 5
关于正态总体均值的假设检验,当总体方差未知时用u检验
 A.
A. B.
B.数学期望反映了随机变量取值的平均水平,方差反映了随机变量取值与其均值的偏离水平
 A.
A. B.
B.如果E(|X|)=0,则P{X=0}=1.
 A.
A. B.
B.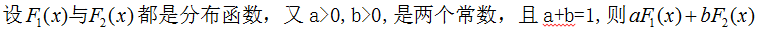 也是一个分布函数
也是一个分布函数
 A.
A. B.
B.设X,Y的方差存在,且不等于0,则D(X+Y)=D(X)+D(Y) 是X,Y独立的必要条件,但不是充分条件
 A.
A. B.
B.
